 Tradycyjnie, jak w każdą środę, rozpoczynam kolejną odsłonę Poradnika maturzysty. Trzecia część poświęcona będzie zadaniom, bo jak wspominałam już nie raz "trening czyni mistrza". Dzisiaj kilka zadań, które są kontynuacją poprzedniego tematu. (LINK)
Tradycyjnie, jak w każdą środę, rozpoczynam kolejną odsłonę Poradnika maturzysty. Trzecia część poświęcona będzie zadaniom, bo jak wspominałam już nie raz "trening czyni mistrza". Dzisiaj kilka zadań, które są kontynuacją poprzedniego tematu. (LINK)
Umówmy się, że każdy spróbuje rozwiązać zadanie sam, a później sprawdzi odpowiedzi, bądź kroki rozwiązania, ok? :)
Gotowi? Zaczynamy!
Zadanie 1.
Przedstaw w postaci nieskracalnego ułamka zwykłego:
Zadanie bardzo proste, pod warunkiem, że potrafimy wykonywać działania na ułamkach, czyli dodawanie, odejmowanie, mnożenie i dzielenie ułamków. Naszym celem jest doprowadzenie do ostatniej formy ułamka, maksymalnie skróconego i bez wyciągniętych całości. W związku z tym, że skupiamy się na powtórkach do matury od tzw. "zera" opiszę każdy krok zadania.
I.
Zamieniamy ułamki na ułamki niewłaściwe, czyli bez wyciągniętych całości. Sprowadzamy do takiej formy, która pozwoli nam dokonywać działań na ułamkach. W przypadku liczby 2,2 zamieniamy ją na ułamek, natomiast cyfrę 2 zostawiamy na razie bez zmian, bo nie wiemy jeszcze jakiego mianownika będziemy potrzebować :)
II.
Mając taką postać można już zamienić liczbę 2,2 na ułamek niewłaściwy. Można pominąć ten krok i wykonać taką zamianę w kroku I.
III.
Teraz przechodzimy do wykonywania działań na ułamkach. Zgodnie z kolejnością działań - jako pierwsze wykonujemy działania w nawiasach, następnie mnożenie/dzielenie i dopiero dodawanie/odejmowanie, więc tak też zrobimy.
Zajmujemy się licznikiem i dodawaniem w nawiasie: w pierwszej kolejności sprowadzamy dwa ułamki do wspólnego mianownika. Jak to zrobić? Otóż znajdujemy jakąś liczbę, która jest wielokrotnością obu mianowników. Spokojnie może nią być liczba 24, bo 6*4 to 24 i jest to wartość drugiego mianownika. Więc zarówno licznik jak i mianownik pierwszego ułamka mnożymy przez 4. Drugi ułamek zostaje bez zmian, ponieważ ma odpowiadający nam mianownik.
Korzystając z okazji zajmijmy się jeszcze dzieleniem z mianownika naszego zadania. Pamiętajmy, że dzielenie jednego ułamka przez drugi to jest mnożenie jednego ułamka przez odwrotność drugiego.
IV.
Teraz spokojnie możemy dodać do siebie ułamki z nawiasu w liczniku naszego zadania, a ułamki z nawiasu w mianowniku naszego zadania możemy pomnożyć przez siebie. W trakcie mnożenia ułamków z mianownika zauważycie, że liczby 22 można ze sobą skrócić i zostaje nam ułamek o mianowniku 3, więc od razu można zamienić cyfrę 2 na ułamek niewłaściwy z mianownikiem 3.
V.
I jak podoba Wam się postać naszego zadania? Wygląda już o wiele lepiej. W kolejnym kroku wymnożymy przez siebie ułamki z licznika, a ułamki z mianownika odejmiemy od siebie, ponieważ mamy już wspólny mianownik zrobiony w poprzednim kroku.
VI.
Pamiętajmy, że kreska ułamkowa to dzielenie. Tak jak wspominałam powyżej, dzieląc jeden ułamek przez drugi, mnożymy jeden ułamek przed odwrotność drugiego.
Jest to już ostatni krok rozwiązywania naszego zadania, bo mamy od razu wynik :) Ale... żeby nie było tak prosto, zanim otrzymamy ostateczny wynik musimy skrócić te ogromne liczby w ułamkach. Bo przecież musimy otrzymać nieskracalną formę ułamka. Jak skracamy? Szukamy wspólnej części w liczniku i mianowniku, przez którą możemy podzielić zarówno licznik jak i mianownik.
Jak ktoś woli zobaczyć całe rozwiązanie zadania bez podzielenia go na części, to prezentuję poniżej.
Zadanie 2.
Porównaj ze sobą liczę a i b:Wydawałoby się, że jest to zadanie, które może sprawić jakąś trudność, ale zapewniam, że wystarczy pomyśleć :)
Żeby sprawdzić, która z liczb jest większa, musimy je uprościć - sprowadzić do porównywalnej postaci. Proponuję się zastanowić, jak może wyglądać podobna, porównywalna postać.
a) Wiemy, że pierwiastek z trzech podniesiony do kwadratu to 3.
b) Wiemy też, że 3 do potęgi czwartej to 81, które trzeba jeszcze podnieść do potęgi 10, czyli już mamy rozwiązanie dla liczby a :)
c) Skoro mamy pierwiastek z trzech do potęgi 82, a wiemy że na jedną cyfrę 3 składa się pierwiastek z trzech podniesiony do potęgi 2, to wiemy już ile wynosi b i mamy poniższe rozwiązanie :)
Zgodnie z powyższym możemy już śmiało wskazać ostateczny wynik: a < b.
Prezentuję całe rozwiązanie zadania:
Zadanie 3.
Która z poniższych liczb jest liczbą niewymierną?Jak rozwiązać to zadanie? Otóż każdą z liczb trzeba doprowadzić do najprostszej postaci. Zacznijmy od liczby a.
I.
W pierwszej kolejności zajmujemy się mianownikiem ułamka, bo widzimy, że jest tam duża liczba pod pierwiastkiem, a to oznacza, że na pewno da się wyciągnąć chociaż z części tej liczby pierwiastek. Jak to zrobić? Sprawdzamy po kolei, chyba że wiecie od razu? Jeśli nie to:
216 : 2 = 108, czy da się wyciągnąć pierwiastek ze 108? Nie. A z 2? Też nie. Idziemy dalej
216 : 3 = 72, czy da się wyciągnąć pierwiastek z 72? Nie. A z 3? Też nie. Idziemy dalej
216 : 4 = 54, czy da się wyciągnąć pierwiastek z 54? Nie. A z 4? Tak i jest to 2. Ale widzimy, że 54 jest dużą liczbą, więc sprawdźmy teraz 54, a o 4 pamiętajmy :)
54 : 2 = 27, czy da się wyciągnąć pierwiastek z 27? Nie i wiemy już, że z 2 też nie, więc sprawdzamy dalej
54 : 3 = 18, czy da się wyciągnąć pierwiastek z 18? Nie i wiemy już, że z 3 też nie, więc kontynuujemy
54 : 4 = 13,5 i tu jedynie wiemy, że z 4 się da ale odpuszczamy w tym przypadku
54 : 5 = 10,8 sprawdzamy dalej
54 : 6 = 9 i tu wiemy, że z 9 da się wyciągnąć pierwiastek i to jest 3.
Tak więc pierwiastek z 216 to pierwiastek z 4 * 9 * 6, czyli inaczej 36 * 6, a to wynosi 6 pierwiastków z 6. Czyli mamy pierwszą postać naszej liczby a:
II.
Zgodnie z zasadą, że przy mnożeniu i dzieleniu można liczby skracać, a widzimy, że i w liczniku i w mianowniku mamy taki sam pierwiastek, więc skrócimy go i otrzymujemy ułamek w postaci:
III.
W pierwszym kroku dzielenie zamienimy na ułamek:
IV.
Kolejnym krokiem jest uporządkowanie licznika, czyli najlepiej doprowadzenie do postaci "wspólnych pierwiastków", tak żeby można było je do siebie dodać/odjąć. Od razu widzimy, że nie ma możliwości zrobić pierwiastka z 10 u każdej z liczb więc zajmijmy się drugą od lewej liczbą i wyciągnijmy pierwiastek:
200 : 2 = 100 i pierwiastek ze 100 wynosi 10, następna liczba
450 : 2 = 225 i pierwiastek z 225 to 15, więc mamy u tych dwóch liczb tzw. "wspólny pierwiastek", zobaczcie:
V.
Robimy porządki, czyli mnożymy 5 * 10 i 3 * 15, następnie te dwa pierwiastki można od siebie odjąć, bo mają swoją "część wspólną", czyli taki sam pierwiastek i tak na prawdę powstaje nam ostatnia postać liczby b:
Teraz można spojrzeć na końcowe wyniki i odpowiedzieć sobie na pytanie z zadnia: która z tych liczb jest niewymierna? Oczywiście prawidłowa odpowiedź to b. Dlaczego? Bo a została doprowadzona do nieskracalnej postaci ułamka zwykłego, a liczba b pozostała w ostatniej formie niewymierna. Ci, którzy sprawnie działają na pierwiastkach wiedzą, że należałoby jeszcze pozbyć się niewymierności z mianownika w liczbie b, czyli pomnożyć zarówno licznik jak i mianownik, przez pierwiastek z mianownika, ale odpuścimy to już sobie :)
Słuchajcie, już trzy zadania za nami :) i niestety ale bardzo się rozpisałam... Pozostałe zadania wrzucam Wam jako pracę domową :) spróbujcie rozwiązać je sami i podeślijcie mi swoje rozwiązania. Możecie zamieścić swoje rozwiązania w komentarzu na blogu, na fejsie, albo w wiadomości prywatnej lub w mailu. Popracujcie sami, a w razie pytań piszcie! Jestem tu codziennie, więc chętnie Wam podpowiem :)
Za tydzień, w kolejnej części poradnika opublikuję rozwiązania zadań z pracy domowej :)
PRACA DOMOWA
a) n * m
b) |m - n|
PS. jakby były problemy z rozczytaniem zdjęć to dajcie znać :)
200 : 2 = 100 i pierwiastek ze 100 wynosi 10, następna liczba
450 : 2 = 225 i pierwiastek z 225 to 15, więc mamy u tych dwóch liczb tzw. "wspólny pierwiastek", zobaczcie:
V.
Robimy porządki, czyli mnożymy 5 * 10 i 3 * 15, następnie te dwa pierwiastki można od siebie odjąć, bo mają swoją "część wspólną", czyli taki sam pierwiastek i tak na prawdę powstaje nam ostatnia postać liczby b:
Teraz można spojrzeć na końcowe wyniki i odpowiedzieć sobie na pytanie z zadnia: która z tych liczb jest niewymierna? Oczywiście prawidłowa odpowiedź to b. Dlaczego? Bo a została doprowadzona do nieskracalnej postaci ułamka zwykłego, a liczba b pozostała w ostatniej formie niewymierna. Ci, którzy sprawnie działają na pierwiastkach wiedzą, że należałoby jeszcze pozbyć się niewymierności z mianownika w liczbie b, czyli pomnożyć zarówno licznik jak i mianownik, przez pierwiastek z mianownika, ale odpuścimy to już sobie :)
Słuchajcie, już trzy zadania za nami :) i niestety ale bardzo się rozpisałam... Pozostałe zadania wrzucam Wam jako pracę domową :) spróbujcie rozwiązać je sami i podeślijcie mi swoje rozwiązania. Możecie zamieścić swoje rozwiązania w komentarzu na blogu, na fejsie, albo w wiadomości prywatnej lub w mailu. Popracujcie sami, a w razie pytań piszcie! Jestem tu codziennie, więc chętnie Wam podpowiem :)
Za tydzień, w kolejnej części poradnika opublikuję rozwiązania zadań z pracy domowej :)
PRACA DOMOWA
Zadanie 1.
Dane są liczby m i n. Oblicz wartości wyrażeń:a) n * m
b) |m - n|
m = 5 - √3
n = 2√3
+ 1
Zadanie 2.
Dana jest liczba x. Wyznacz liczbę, której 60% jest równe x. Wynik podaj z dokładnością do 0,01.
x = (8/5)-1 + (1/2)3 * [2/3 * 5 – (11/23)0]
Uwaga! znak "/" oznacza kreskę ułamkową.
Zadanie 3.
Oblicz wartość liczby k, wiedząc, że:
k = log216
Zadanie 4.
Cena pewnego towaru wraz z 7-procentową stawką podatku VAT była równa 64,20 zł. Oblicz cenę tego towaru, gdyby stawka podatku VAT była równa 22%.PS. jakby były problemy z rozczytaniem zdjęć to dajcie znać :)









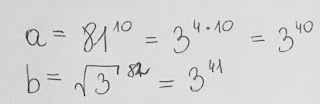






super, kupiłem sobie różowe kompedium, bo było po 5zł, i ciężko było ruszyć, dzięki!
OdpowiedzUsuń